Spotify’s New Experimentation Coordination Strategy

At Spotify we run hundreds of experiments at any given time. Coordinating these experiments, i.e., making sure the right user is receiving the right “treatment” with a population of hundreds of millions of users, poses technical challenges. Adding to the complexity, some of these experiments must be coordinated in the sense that the same user cannot be in two experiments at the same time. These are well-known problems among tech companies — take, for example, Google’s solution in Tang et al (2010). But the statistical implications of different solutions have not been properly investigated. In a recent paper (M. Schultzberg, O. Kjellin, and J. Rydberg, 2020), we investigate important statistical properties of a common technical solution to the coordination — called “Bucket Reuse”. In this blog post we highlight some interesting results and present some details about how Spotify will coordinate experiments from now on.
What is Bucket Reuse?
Bucket Reuse is a simple idea utilizing the power of hashing. Essentially the steps are as follows: decide on a number of buckets (B). Take the unique user ID and hash it together with a random salt into B “buckets” such that all users hash into one and only one bucket. Once the hash map is established, all sampling is performed on the bucket level. This implies that a bucket either is or is not in a sample at any given time point. If we want to sample N number of users, we sample the number of buckets that contain the number of users closest to the desired number N. If, e.g., the desired N is 20 and each bucket contains 3 users, we would sample 7 buckets and end up with 21 users. Note that a bucket is simply a logical group of units to which we assign a certain user by a fixed hash map. Figure 1 illustrates such a map. The second part of the name Bucket Reuse comes from the fact that we reuse the same buckets over and over again in the sampling for all experiments. That is, the random salt for the hashing is selected only once; after that, the hash map and the number of buckets is fixed. Importantly, when we talk about Bucket Reuse for experimentation, we always mean the following: the random sampling is performed on the bucket level; the random treatment allocation is performed at the user level on the users in the sample.
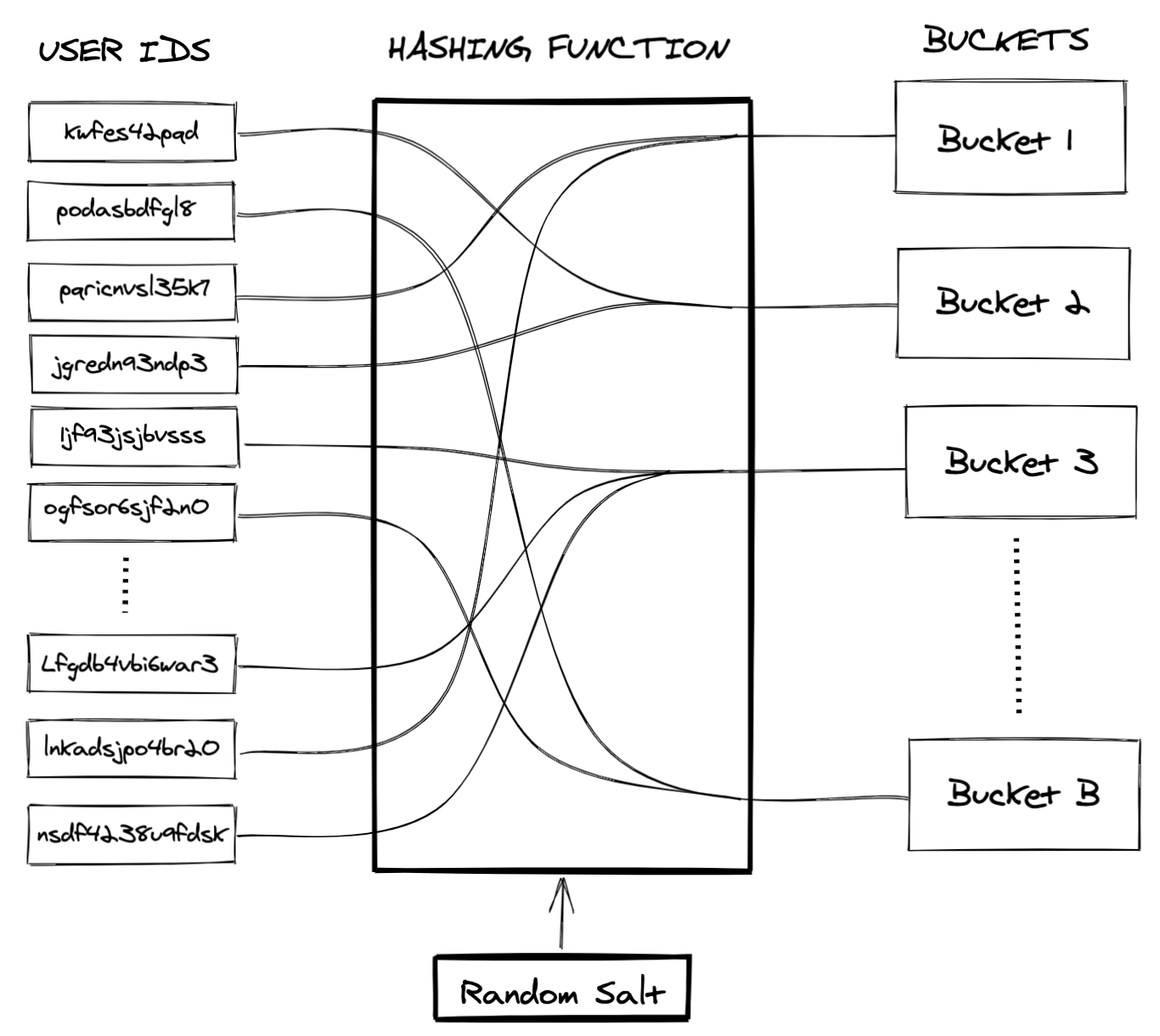
Figure 1: Schematic illustration of a hash map. A user ID is hashed together with a random salt to map each user to a unique bucket.
What is experiment coordination?
To get into the interesting parts of experiment coordination, we need to establish some key concepts. Figure 2 illustrates the concepts of exclusive and nonexclusive experiments. That two or more experiments “are exclusive” to each other simply means that they are run on distinct sets of users. Experiments that are nonexclusive are nonexclusive to all experiments at Spotify, meaning that they all randomly overlap in terms of users.
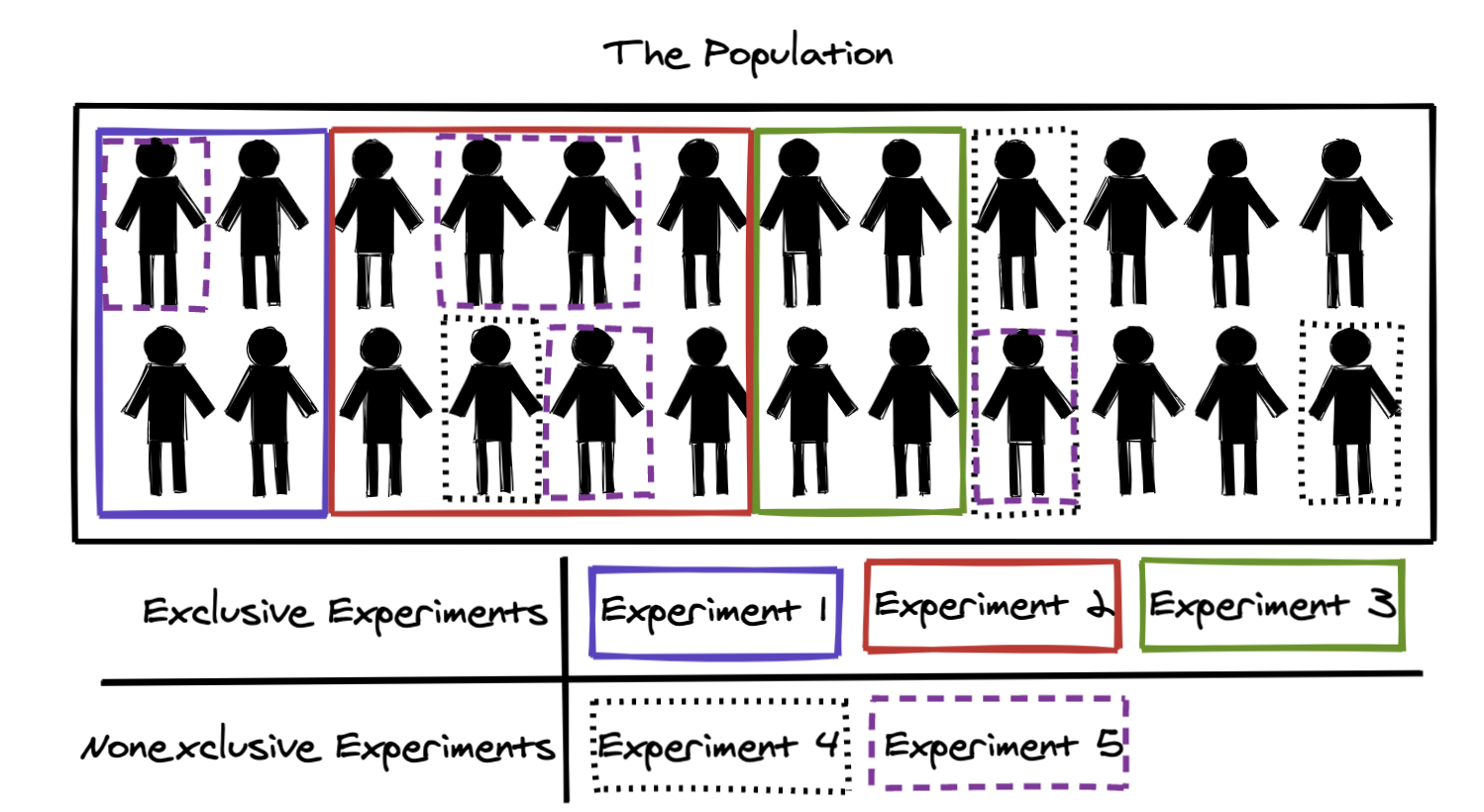
Figure 2: Illustration of exclusive and nonexclusive experiments. Exclusive experiments never overlap with each other in terms of users; nonexclusive experiments randomly overlap with exclusive experiments and other nonexclusive experiments. Note that the allocations in this figure were selected for illustration; in a true random sample we would expect exclusive experiments to also be spread out uniformly.
The most critical challenge from a statistical perspective is imposed by what we call programs of exclusive experiments. A program of exclusive experiments is a set of experiments run over time where all simultaneous experiments are exclusive to each other. That is, a unit is in at most one, and only one, of the experiments in the program at any given time point. At Spotify we have such programs for several surfaces in the app, for example Search, the Home screen, and certain parts of the backend code base. To better understand the limitations imposed on the sampling by running programs of exclusive experiments, it is helpful to introduce the concepts of paths. A path is simply a sequence of experiments that a unit can be in. Figure 3 illustrates a program of exclusive experiments containing 5 experiments over time. Below the experiments, their possible paths are displayed. For example, it is not possible to go through both Experiments 3 and 4 as they overlap in time and are exclusive, and must therefore be run on distinct users. The number of unique possible paths explodes combinatorially after a relatively short time period in most programs, and only a small partition of the possible paths can be taken by any unit regardless of the sample strategies discussed in this post.
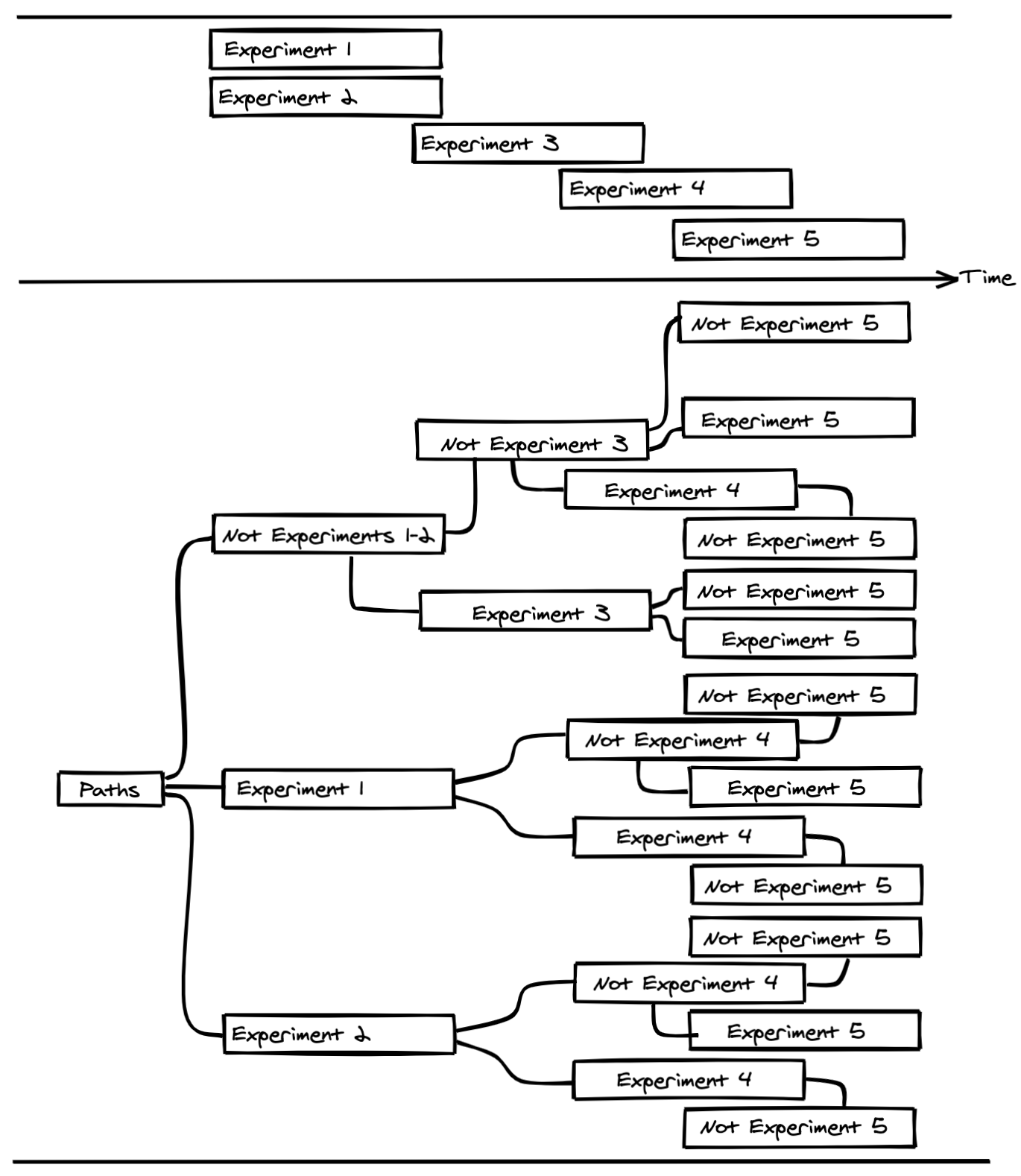
Figure 3: Paths of experiences possible during a hypothetical program of 5 exclusive experiments.
Highlights from Schultzberg et al.
Schultzberg et al. presents two key results:
Under unrestricted sampling of buckets, i.e., Bucket Reuse in nonexclusive experiments, the properties of the difference-in-means estimator of the average treatment effect is approximately equivalent to the properties under random sampling of units. In other words, standard t-tests can be used for inference. The key to this remarkable finding is connecting Bucket Reuse to the existing literature on randomized experiments embedded in complex sampling designs (Horvitz and Thompson, 1952; van den Brakel and Renssen, 2005).
The bias imposed by the restricted sampling of buckets implied by programs of exclusive experiments is derived. It is shown that this bias is often restricted to the history right before the experiment. Moreover, the length of the window of the history that affects the bias can be estimated for any empirical experimentation program. One way to phrase this finding is that the sample at a time point T is not random with respect to the last D days leading up to time T, but random with respect to everything that happened before the time point T-D. If things happened during the last D days that make the set of buckets available for sampling at time T different from the population with respect to the treatment effect, the estimator is biased. This insight makes it possible for experimenters to evaluate the risk for biases by checking what experiments have been run in the program over the last D days, and if those risks for biases are likely to affect the average treatment effect in the experiment that is about to be started.
Spotify’s new experimentation coordination strategy
We have migrated our experimentation platform to using Bucket Reuse for all experiments at Spotify. There are a few key reasons why we prefer Bucket Reuse over other solutions:
It is simple to implement and understand.
It is a technically feasible solution that allows us to do complex coordination without losing speed in our systems. As new users come into Spotify, they are uniformly hashed into the existing buckets — that is, the system scales as Spotify’s user base grows.
Using one company-global bucket structure makes it easy to coordinate experiments arbitrarily. For example, two programs that have been run independently can easily be merged into one program of exclusive experiments at any time point for any period of time. And, a sample from a previous experiment with a broken experience can easily be quarantined and avoided in any future experiments, as the sampling units are always the same over time.
At Spotify we have chosen Bucket Reuse with 1M (1,000,000) buckets to coordinate all experiments. That is, all users are hashed into 1M buckets, and these buckets are used for all experiments in all experimentation programs, exclusive and nonexclusive. Although Schultzberg et al. establishes that smaller numbers of buckets can have statistical properties enabling straight forward inference, it should be clear that the larger the number of buckets, the better. Even though the inference for the average treatment effect is unaffected by the bucket sampling, it is well known that the effect of cluster sampling on other estimands decreases when the number of buckets increases (Kumar Pradhan). That is, imposing a bucket structure is not preferred from a statistical perspective, but it is a technical necessity. The choice of 1M buckets was made because it is close to the largest number of buckets we can have while still keeping the selected buckets within an executable script stored in a database without having to resort to BLOB storage.
We are not planning to have any full stops or to reshuffle users into new buckets. However, there are naturally occurring periods of low experimentation that will help decrease the dependency between the samples in programs of exclusive experiments. For example, many programs run fewer general product experiments over the winter holidays due to unusual listening behaviors. These natural pauses effectively reset the programs in terms of dependencies.
To help experimenters running programs of exclusive experiments, we are implementing a few tools to keep track of the short-term dependencies. For each program, we will estimate the length of the history that can bias the results. Moreover, we are also implementing a tool to see the history of the available buckets at any time point. Figure 4 displays a prototype of this tool. It allows experimenters to evaluate if the experiments that the available user came out of are likely to bias the estimator in their experiment. It also provides information about the size of the overlap with previous experiments.
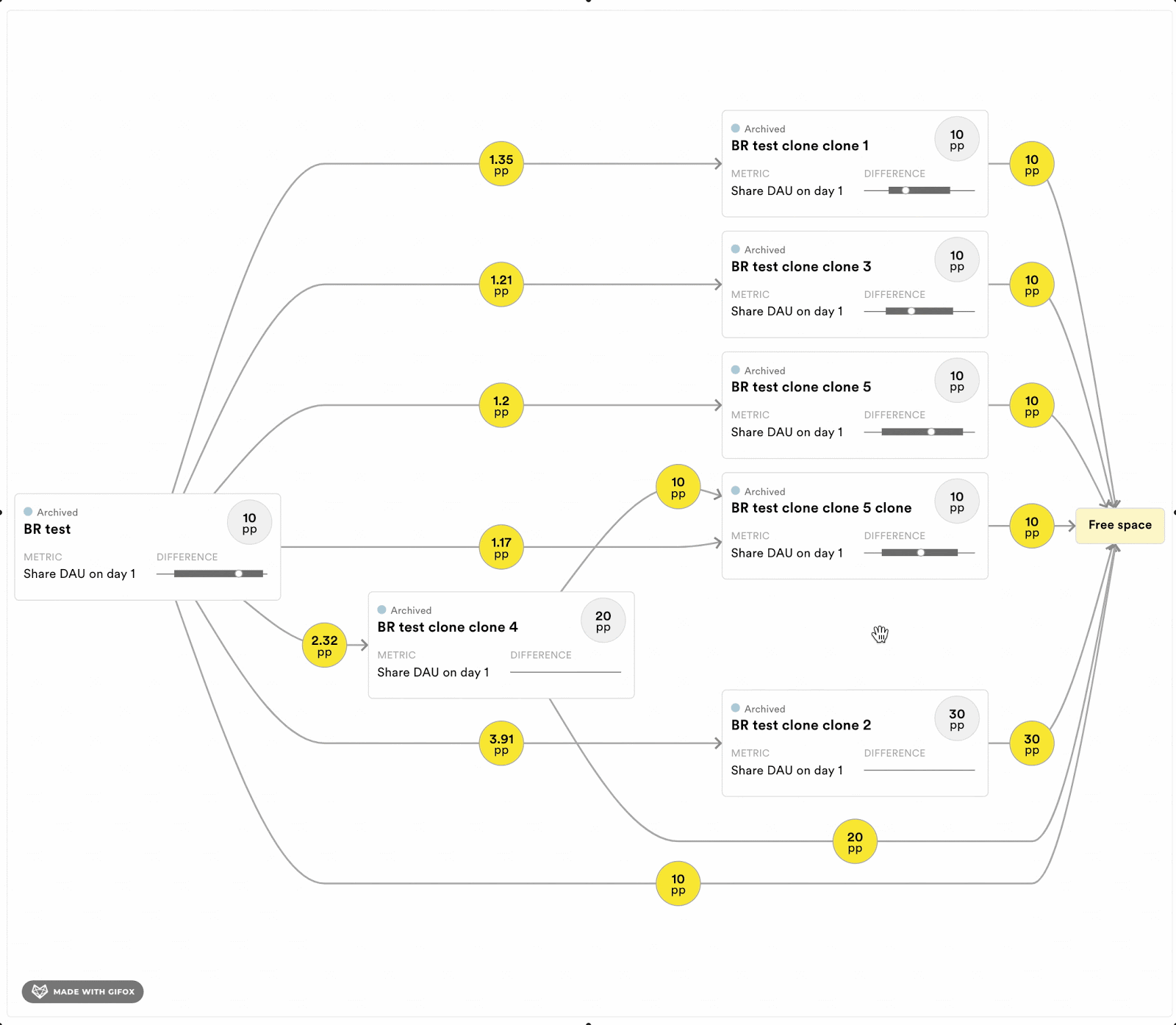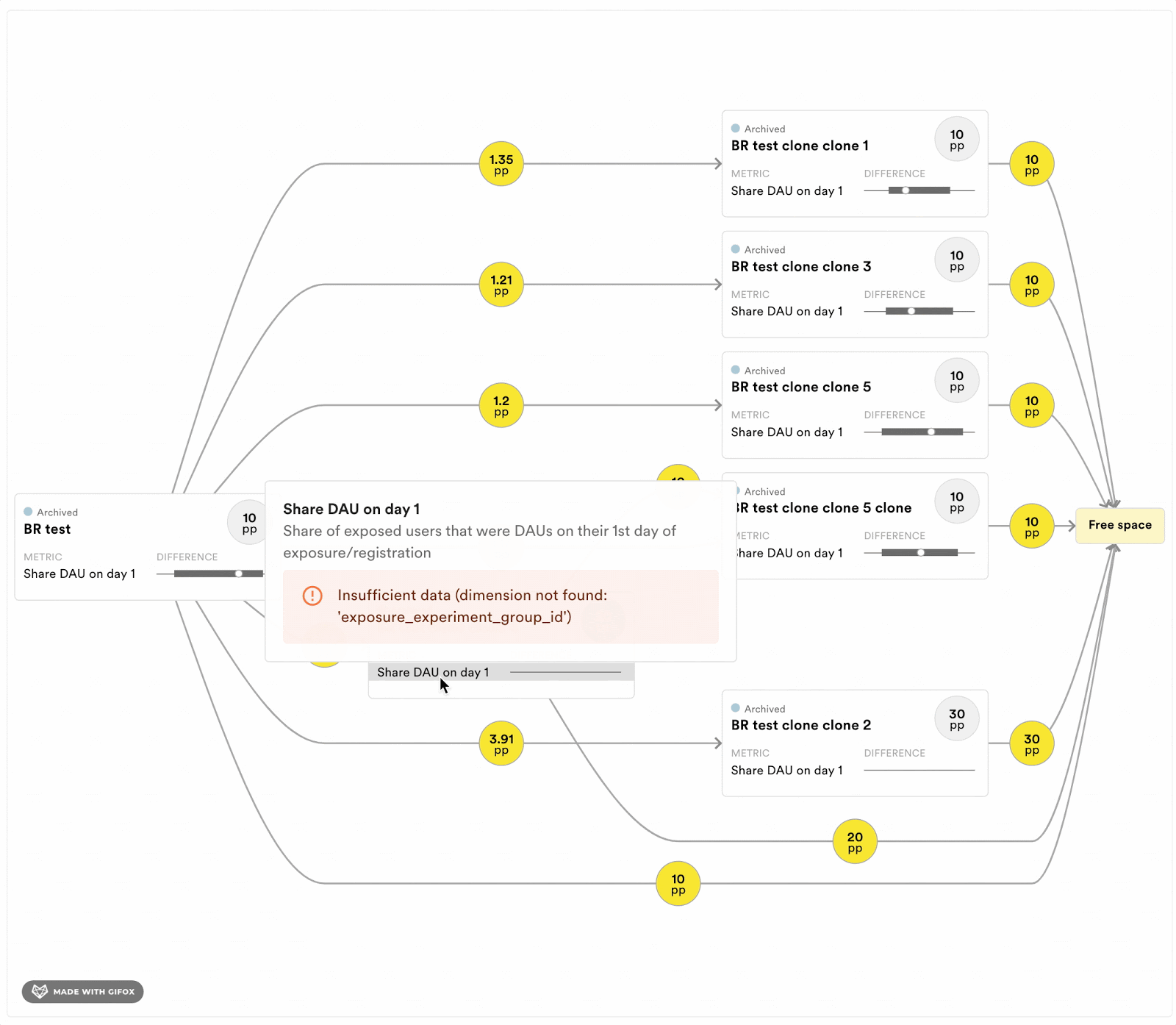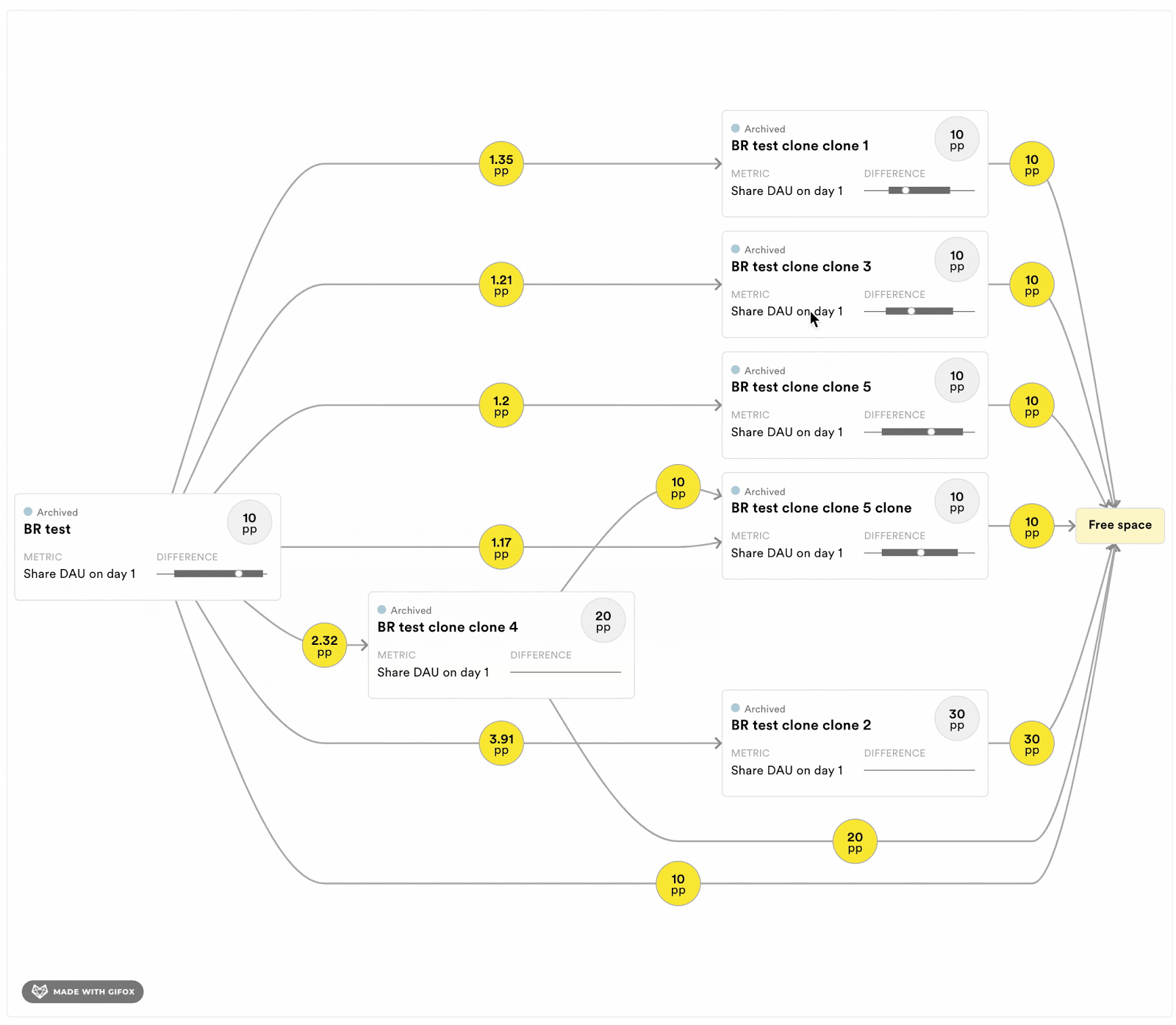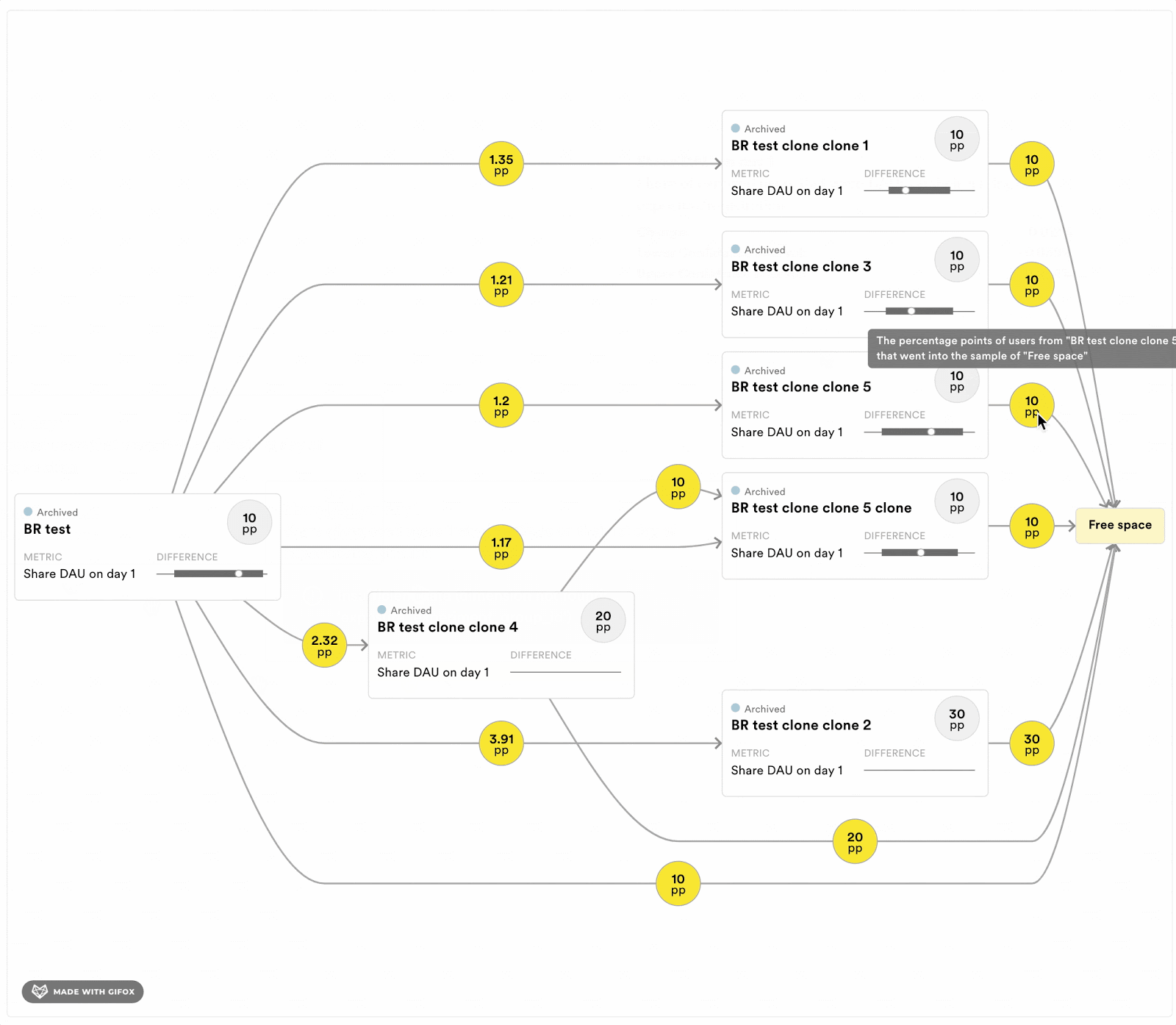
Figure 4: Dependency graph that shows the experimenter where the free space, and thereby their sample, will come from in terms of previous experiments in the exclusive program. Each rectangle corresponds to a previously run experiment. The numbers in the yellow circles indicate the percentage points of the population that went from one experiment into another, and finally into the proportion of the population that is available (“free space”) for sampling right now. The experimenter can see what effects the previous experiments had on the metrics of interest in their experiment.
Figure above for illustrative purposes only.
Conclusion
Statistical validity, derived from proper random sampling and random treatment allocation, is the cornerstone of a successful experimentation program. However, implementing systems that can serve hundreds of experiments to hundreds of millions users — while retaining the ability to conveniently coordinate experiments to be exclusive, without overlap — requires compromises between technical feasibility and statistical properties. At Spotify, we have migrated the internal experimentation platform to rely fully on bucket reuse, a technically desirable solution that provides speed, simplicity, and flexibility. In this post we establish the statistical properties under bucket reuse and conclude that the validity is unaffected. This migration enables more experiments of higher quality at Spotify.
Experimentation Platform team, Spotify
References
Brakel, Jan van den, and Robbert H. Renssen. “Analysis of Experiments Embedded in Complex Sampling Designs.” Survey Methodology 31, no. 1 (2005): 23–40.
Horvitz, D. G. and D. J. Thompson. “A Generalization of Sampling Without Replacement from a Finite Universe.” Journal of the American Statistical Association 47, no. 260 (1952): 663–685. https://doi.org/10.2307/2280784
Kumar Pradhan, Bijoy. “On efficiency of cluster sampling on sampling on two occasions.” Statistica 64, no. 1 (2004): 183–191. https://doi.org/10.6092/issn.1973-2201/31
Schultzberg, Mårten, Oskar Kjellin, and Johan Rydberg. “Statistical Properties of Exclusive and Non-exclusive Online Randomized Experiments using Bucket Reuse.” arXiv preprint arXiv:2012.10202 (2020).
Tang, Diane, Ashish Agarwal, Deirdre O’Brien, and Mike Meyer. “Overlapping experiment infrastructure: more, better, faster experimentation.” KDD ’10: Proceedings of the 16th ACM SIGKDD international conference on Knowledge discovery and data mining, (July 2010): 17–26.



