Comparing Quantiles at Scale in Online A/B Testing

March 23, 2022 Published by Mårten Schultzberg (Senior Data Scientist) and Sebastian Ankargren (Data Scientist)

TL;DR: Using the properties of the Poisson bootstrap algorithm and quantile estimators, we have been able to reduce the computational complexity of Poisson bootstrap difference-in-quantiles confidence intervals enough to unlock bootstrap inference for almost arbitrary large samples. At Spotify, we can now easily calculate bootstrap confidence intervals for difference-in-quantiles in A/B tests with hundreds of millions of observations.

Why are quantiles relevant for product development?

In product development, the most common impact analysis of product changes is often summarized by the change in the average of some metric of interest. This is a natural measurement, since changes in an average, in many contexts, map more or less directly to changes in business value. In addition, averages have convenient mathematical properties that make it straightforward to quantify uncertainty in over-served changes.

For a product development team to understand the impact of their work and be able to make strategic decisions, averages are not always sufficient. It is often of interest to understand how users with different behaviors are reacting to product changes. For example, a change in app load time often has the biggest impact on users with the slowest devices. Another example is app engagement — if our goal is to increase app engagement, it is often of interest to see if the engagement of the least engaged users increased, or if it was only users that were already highly engaged that increased their engagement more. For this purpose, quantiles and changes in quantiles, i.e., difference-in-quantiles due to product changes, is a powerful complement to the average. However, quantiles have less neat mathematical properties, which makes it less straightforward to quantify the uncertainty in observed changes in quantiles analytically. One robust method for quantile inference is bootstrap.

What is (Poisson) bootstrap inference?

Bootstrap inference is an ingenious resampling-based strategy for non-parametrically estimating the sampling distribution of any statistic using only the observed sample at hand. Bootstrap was originally proposed by the statistical legend Bradley Efron (Efron, 1979). Since the original paper, many extensions of the original idea have been developed, and their properties studied under various conditions for various test statistics.

Standard statistical inference describes how an estimator, such as the sample mean, would behave if the experiment that produced the observed data were to be repeated over and over again. For many simple estimators, like the sample mean, what the behavior is like when the experiment is repeated can be described mathematically, and inference can easily be made. However, for some statistics like quantiles or ratios of means, it is often not possible to describe the sampling distribution analytically. In these situations, the bootstrap is a powerful tool. The idea of the bootstrap is almost painfully simple as it uses the same idea of repeating the experiment, but without having to mathematically derive what will happen. Simply put, instead of viewing the observed data as a sample from a population, bootstrap views the sample as the population. The ingenuity of this framing is that in order to describe the behavior of an estimator, we just need to take samples from our (pseudo)population — our experimental sample. Bootstrapping thus simply amounts to resampling observations from the observed sample with replacement, recording the estimate, and repeating this procedure. The collection of estimates describes the sampling distribution of the estimator from which inference can be made.

To fully appreciate the idea, let’s assume we have observed a sample consisting of five observations: 4, 8, 11, 13, 15. To use bootstrap inference, we randomly draw five observations from our sample with replacement. Table 1 shows the results from 10 bootstrap replications. In the first resample, we obtain the observations 11, 11, 13, 13, 15. The sample median in this bootstrap sample is 13, which we record. Repeating this resampling step a large number of times provides us with a characterization of the sample median’s sampling distribution through the array of bootstrap sample medians found at the bottom of Table 1. The table shows results from 10 resamples, but in practice the number of resamples is usually in the thousands. A (1-alpha)100% level confidence interval can be computed by finding the alpha/2 and (1-alpha/2) quantiles of the bootstrap sample medians.

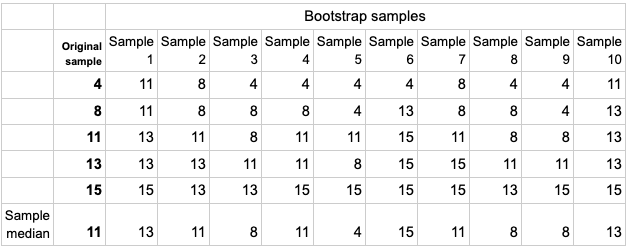
Table 1: Example of bootstrap distribution of the sample median for a sample of 5 units over 10 bootstrap samples.

The validity of bootstrap is well studied for a large class of statistics. See, for example, Ghosh et al. (1984) and Falk and Reiss (1989) for details regarding quantiles.

Computational challenge

The computationally intensive nature of bootstrap caused by repeated resampling has made the primary use case small-sample experiments. For big data experiments, like A/B tests in the tech industry with millions and even hundreds of millions of users, bootstrap inference was for many years intractable unless only a fraction of the total number of observations was considered. Recently, Poisson bootstrap (Hanley and MacGibbon 2006, Chamandy et al. 2012) has gained traction as a computationally efficient way of approximating the original bootstrap’s sampling with replacement with big data, at least for linear estimators such as means.

The computational challenge of bootstrap inference is obvious. The Poisson bootstrap was proposed not because it is less computationally complex but because it is easier to implement in a scalable fashion for some estimators. For example, Chamandy et al. showed how Poisson bootstrap inference can be implemented with map-reduce (Dean and Ghemawat, 2008). Another approach that enables fast implementations of quantile bootstrap is the so-called “Little bag of bootstrap” (Kleiner et al., 2014). This approach also utilizes Poisson bootstrap, but the computational challenge is handled by splitting the full sample problem into smaller samples, performing calculations and then combining the results to yield the full sample results. Most tech companies have avoided bootstrap inference for quantiles altogether, and are instead relying on parametric approximations with analytical solutions. An exception includes bootstrapping based on compressed data, as described for example in the Netflix blog posts on practical significance and data compression. Most approximations are based on the normal distribution, see for example this blog post that uses results from Liu et al. (2019). However, as for any parametric test, the robustness of such approximations is highly dependent on the data-generating process.

Interestingly, as we will discuss in the next section, there are other properties of the Poisson sampling and the quantile estimators themselves that can be used to reduce the complexity of the bootstrap algorithm to the extent that it will almost always be possible to perform bootstrap inference for quantiles and difference-in-quantiles without complex implementations.

Our new algorithm: Bootstrapping without resampling

To understand our proposed algorithm, one must understand the class of quantile estimators we are studying. There are many ways to estimate a sample quantile; most include some form of weighting of the closest order statistics. We propose to use a slightly more crude estimator. Let the quantile of interest be q and the sample size be N. If (N+1)q is an integer, the corresponding order statistic is our estimator. If (N+1)q is not an integer, we randomly select between the two neighboring integers. For example, assume we are interested in the median, and N=101. Then the 51st observation in the ordered list of observations is our median estimate. If N=100, then (N+1)q=50.5, and either the 50th or the 51st observation is, with equal probability, our median estimate.

Our big realization was that to enable a faster algorithm, the only thing we need in order to estimate the bootstrap sample quantile is to know what index from the original sample becomes the bootstrap sample quantile in each Poisson-generated sample. The naive (and computationally complex) way of doing this is to repeat each observation in the original sample Poi(1) number of times, and check which observation had the ordered index that corresponded to the quantile. Our proposal is to instead study the distribution of the index in the original sample that is recorded as the quantile of interest in the bootstrapped sample. If you look at Table 1 again, you can see that the indexes of the ordered observations that wound up as the bootstrap-sample medians are 4,3,2,3,1,5,3,2,2,4. That is, the value 4 (ordered index 1), was only median in one bootstrap sample. The value 8 (ordered index 2) was median in three bootstrap samples, the value 11 (ordered index 3) was median in 3 samples, etc. Naturally, the closer the index is to that of the original sample median, the more frequently the value becomes the bootstrap sample median.

Let’s look closer at the distribution of ordered indexes selected across repeated bootstrap samples. We consider a sample of size N=200, and suppose that we are interested in the 20th percentile, that is q=0.2. Figure 1 displays the frequencies at which indexes of observations in the ordered original sample were recorded as the 20th percentile in 1M Poisson bootstrap samples.

Figure 1: Frequencies at which indexes of observations in the ordered original sample were recorded as the 20th percentile in 1M Poisson bootstrap samples.

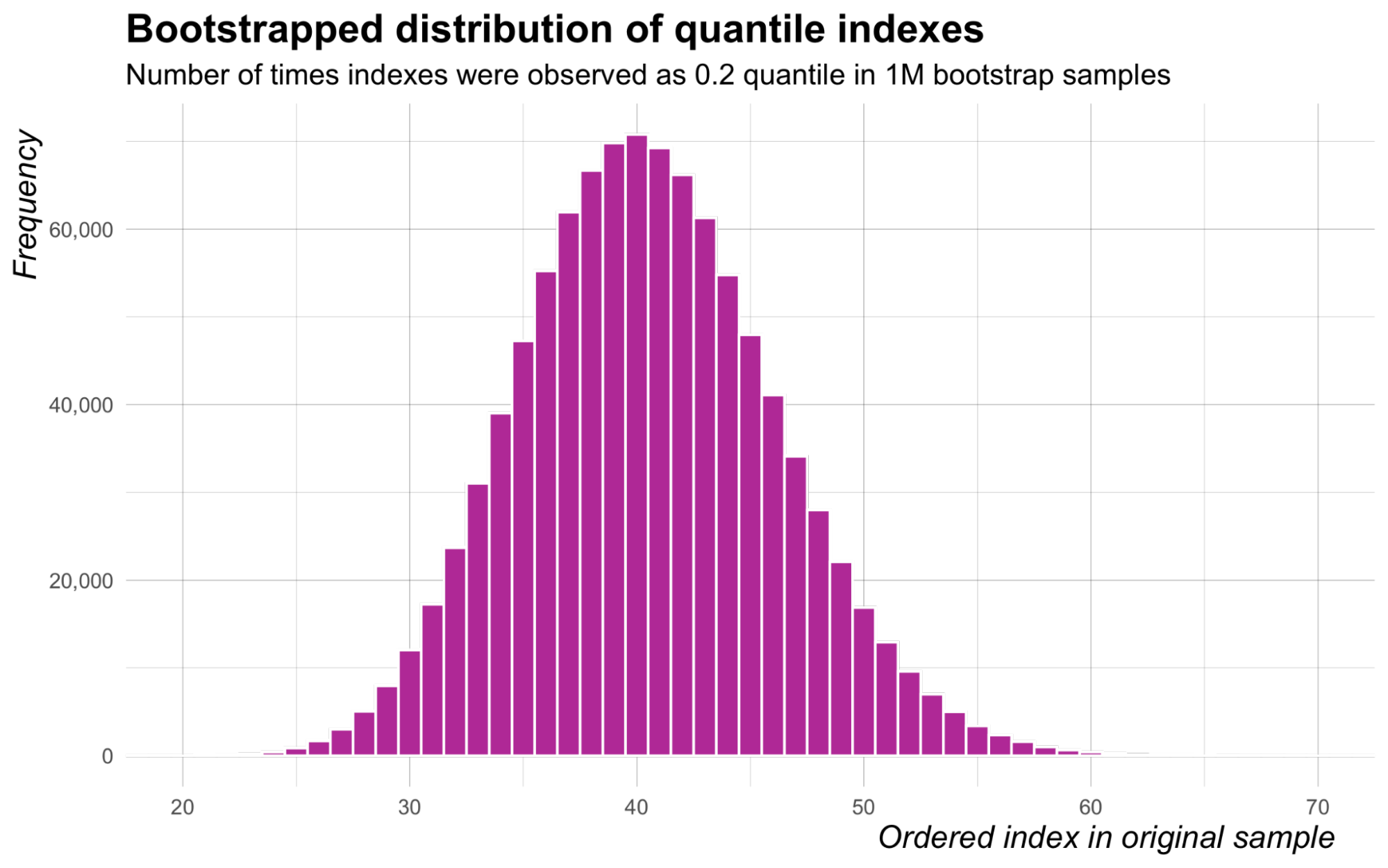
There are two important learnings from this figure. First, most ordered indexes between 1 and 200 are never found to be the bootstrap sample quantile. This is of course expected, but it means that we are generating Poisson values (resampling) for many order statistics that will never have a chance to be the sample quantile. The second learning is far more important — the distribution highly resembles a binomial distribution. It turns out that the distribution of ordered indexes in the original sample of size N that are recorded as the qth sample quantile in Poisson-generated bootstrap samples is very well approximated by a Bin(N+1,q) distribution for large N.

For the difference-in-quantile confidence intervals, the implications from this result are profound. Computationally, it means that for a difference-in-quantiles bootstrap confidence interval we can sort the outcomes once, and then sample indexes and use the corresponding ordered observations as bootstrap estimates for the quantile. If you are interested in the details regarding the reduction in complexity, see our paper Schultzberg and Ankargren (2022).

Interestingly, for one-sample quantile bootstrap confidence intervals, our result is rediscovering the well known order-statistic based confidence intervals for quantiles, see for example Gibbons and Chakraborti (2010), but derived from the bootstrap approach. The important difference is that we are not only interested in the confidence intervals themselves, but the distribution of indexes. Ultimately, this is what enables us to do two-sample comparisons.

The Python code block below illustrates how simple it is to calculate a bootstrap confidence interval for a sample quantile estimator using the binomial approximation of the index distribution.

import numpy as np
from scipy.stats import binom

alpha=.05
quantile_of_interest=0.5
sample_size=10000
number_of_bootstrap_samples=1000000
outcome_sorted = np.sort(np.random.normal(1,1,sample_size))

ci_indexes = binom.ppf([alpha/2,1-alpha/2],sample_size+1, quantile_of_interest)
bootstrap_confidence_interval = outcome_sorted[[int(np.floor(ci_indexes[0])), int(np.ceil(ci_indexes[1]))]]

f"The sample median is {np.quantile(outcome_sorted, quantile_of_interest)}, the {(1-alpha)*100}%\
confidence interval is given by ({bootstrap_confidence_interval})."

For the one-sample case, the complexity consists of a single sort of the original outcome data (actually this can be simplified even further). This follows since we already know which order statistics will be boundaries for the alpha/2 and 1-alpha/2 tails of the binomial distribution of indexes that will become the quantile of interest in the distribution of bootstrap estimates.

For the two-sample case, which is our main contribution, we still need to calculate the difference between the two sample quantiles in each bootstrap iteration. The Python code block below illustrates how simple it is to calculate a bootstrap confidence interval for a difference-in-quantiles estimator using the binomial approximation.

import numpy as np from numpy.random import normal, binomial alpha=.05 quantile_of_interest=0.5 sample_size=10000 number_of_bootstrap_samples=1000000 outcome_control_sorted = np.sort(normal(1,1,sample_size)) outcome_treatment_sorted = np.sort(normal(1.2,1,sample_size)) bootstrap_difference_distribution = outcome_treatment_sorted[binomial(sample_size+1, quantile_of_interest, number_of_bootstrap_samples)] - outcome_control_sorted[binomial(sample_size+1, quantile_of_interest, number_of_bootstrap_samples)] bootstrap_confidence_interval = np.quantile(bootstrap_difference_distribution,
[alpha/2 , 1-alpha/2])

f"The sample difference-in-medians is \
{np.quantile(outcome_treatment_sorted, quantile_of_interest)-np.quantile(outcome_control_sorted, quantile_of_interest)},\
the {(1-alpha)*100}% confidence interval for the difference-in-medians is given by ({bootstrap_confidence_interval})."

It is easy to verify that these binomial-approximated confidence intervals give similar results as the usual bootstrap confidence intervals, and that they are statistically valid. For example, the code below shows a Monte Carlo simulation of the false positive rate for a one-sided bootstrap confidence interval for the sample median.

import numpy as np
from scipy.stats import binom

alpha=.05
quantile_of_interest=0.5
sample_size=10000
number_of_bootstrap_samples=1000000
replications = 10000

bootstrap_confidence_intervals = []
ci_index = int(np.floor(binom.ppf(alpha,sample_size+1,
quantile_of_interest)))
for i in range(replications):
outcome_sorted = np.sort(np.random.normal(0,1,sample_size))
bootstrap_confidence_intervals.append(outcome_sorted[ci_index])

f"The empirical false positive rate of the test using the bootstrap confidence interval is {np.mean([1 if i>0 else 0 for i in bootstrap_confidence_intervals])*100}%, the intended false positive rate is {alpha*100}%"

A faster Julia script to run comparison simulations for the difference-in-quantiles case can be found in this GitHub repository.

Just to give a feeling for the impact of this reduction, we ran some benchmarks of our implementation in Julia. For a two-sample median confidence interval, where the total sample size is 2,000 and we draw 10,000 bootstrap samples, the standard Poisson bootstrap implementation (realizing each bootstrap sample) has a median runtime of 1,821 milliseconds, using 2.4 GB of memory. The corresponding binomial-based confidence interval function takes 2.2 milliseconds, using 407 KiB of memory.

SQL implementation

A simple and powerful SQL+Python implementation of our proposed binomial-based quantile bootstrap confidence interval is the following:

Step 1: [In Python] Calculate the indexes that correspond to the alpha/2 upper and lower tail on the Binom(N+1,q) distribution.

Step 2: [In SQL] Return the order statistics from the outcome according to the indexes from Step 1 as the confidence interval for the quantile.

Conclusion

Having robust and assumption-free inference methods for various types of estimators is critical for proper evaluation of A/B tests and risk management for product decisions. Using our new index-based bootstrap algorithm, we have simplified the computation of bootstrap confidence interval estimates for difference-in-quantiles sufficiently to be plausible for all sizes of data. This unlocks an important inference tool for A/B tests and dashboards at Spotify.

References:

Chamandy, N., Omkar Muralidharan, Amir Najmi, and Siddartha Naidu.“Estimating uncertainty for massive data streams.” Technical report, Google, (2012) https://static.googleusercontent.com/media/research.google.com/en//pubs/archive/43157.pdf

Dean, J. and Sanjay Ghemawat. “MapReduce: Simplified Data Processing on Large Clusters.” Communications of the ACM, 51(1):107–113 (2008). https://doi.org/10.1145/1327452.1327492.

Efron, Bradley. “Bootstrap Methods: Another Look at the Jackknife.” The Annals of Statistics, 7 (1) 1 – 26, January, 1979. https://doi.org/10.1214/aos/1176344552

Falk, M. and R.-D. Reiss. “Weak Convergence of Smoothed and Nonsmoothed Bootstrap Quantile Estimates.” The Annals of Probability, 17(1):362–371 (1989). https://doi.org/10.1214/aop/1176991515

Ghosh, M., William C. Parr, Kesar Singh, and G. Jogesh Babu. “A Note on Bootstrapping the Sample Median.” The Annals of Statistics, 12(3):1130–1135 (1984). https://doi.org/10.1214/aos/1176346731.

Gibbons, J.D. and Subhabrata Chakraborti. Nonparametric Statistical Inference (5th ed.). Chapman and Hall/CRC, (2010). https://doi.org/10.1201/9781439896129

Hanley, J. A. and Brenda MacGibbon. “Creating non-parametric bootstrap samples using Poisson frequencies.” Computer Methods and Programs in Biomedicine, 83:57–62 (2006). http://www.med.mcgill.ca/epidemiology/Hanley/Reprints/bootstrap-hanley-macgibbon2006.pdf

Kleiner, A., Ameet Talwalkar, Purnamrita Sarkar, and Michael I. Jordan. “A scalable bootstrap for massive data.” Journal of the Royal Statistical Society, Series B (Statistical Methodology), 76(4):795–816 (2014). https://doi.org/10.1111/rssb.12050

Liu, M., Xiaohui Sun, Maneesh Varshney and Ya Xu. “Large-Scale Online Experimentation with Quantile Metrics.” arXiv e-prints, art. arXiv:1903.08762 (2019). https://arxiv.org/abs/1903.08762

Schultzberg, M. and Sebastian Ankargren. “Resampling-free bootstrap inference for quantiles.” arXiv e-prints, art. arXiv:2202.10992, (2022). https://arxiv.org/abs/2202.10992. Accepted for Publication in the Proceedings of the Future Technologies Conference 2022.

Tags: experimentation