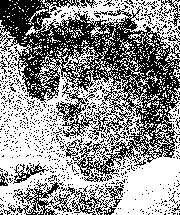How to shuffle songs?
At Spotify we take user feedback seriously. We noticed some users complaining about our shuffling algorithm playing a few songs from the same artist right after each other. The users were asking “Why isn’t your shuffling random?”. We responded “Hey! Our shuffling is random!”
So who was right? As it turns out, both we and the users were right but it’s a bit more complicated than that. It also tells a nice story about how to interpret users’ feedback.
Our perspective
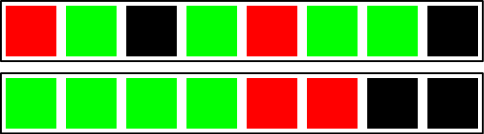
Since the Spotify service launched, we used Fisher-Yates shuffle to generate a perfectly random shuffling of a playlist. However, perfectly random means that the following two orders are equally likely to occur (different colors represent different artists):A side note: I think Fisher-Yates shuffle is one of the most beautiful random algorithms and it’s amazing that such complicated problem can be solved in 3 lines of code in some programming languages. And this is accomplished using the optimal number of operations and optimal amount of randomness.
Gambler’s fallacy
At first we didn’t understand what the users were trying to tell us by saying that the shuffling is not random, but then we read the comments more carefully and noticed that some people don’t want the same artist playing two or three times within a short time period.
It is known that we humans are sometimes bad at estimating probabilities. Suppose that you use a coin every day at work to decide where to eat lunch. The first four days of the week the coin decided that you should eat Thai food, but you prefer Indian. You might think “The coin decided four times this week in favor of Thai, it must be Indian today”.
If you think the coin has higher probability of deciding for Indian on Friday, you are wrong. Throwing the coin for a millionth time is the same as throwing it for the first time. After all, it is just a simple coin, it has no memory, doesn’t know who threw it, etc. So both heads and tails have the same probability on Friday – 50%.
Another example: people often think that if they haven’t won anything in a scratchcard lottery a couple of times in a row, they should have bigger chance of winning now. This phenomenon is called Gambler’s fallacy and it’s the same fallacy that lead to the mistake about Thai/Indian food.
Let’s go back to our users who have also fallen victims to Gambler’s fallacy. If you just heard a song from a particular artist, that doesn’t mean that the next song will be more likely from a different artist in a perfectly random order. However, the old saying says that the user is always right, so we decided to look into ways of changing our shuffling algorithm so that the users are happier. We learned that they don’t like perfect randomness.
The algorithm
It seemed like a problem that must have been solved by somebody else before. Indeed, we found a blog post The art of shuffling music by Martin Fiedler that solves precisely the same problem. However, his algorithm is complicated and could be very slow in some cases, so we modified it to better suit our needs.
The main idea is very similar to the methods used in dithering. Suppose we have a black and white picture that uses a few hundred shades of gray.
We would like to simplify the picture even further by using only pixels of two colors, black and white. We could use random sampling: say a pixel has an 80% shade of gray, then it will have 80% chance of becoming black and 20% chance of becoming white. We process pixels one by one and for each one we randomly decide its new color based on the original shade of gray. However, the result is very far from satisfactory.
As you can see, the black pixels form clusters and there are also big white spots. It would be better if the black and white spots were spread out more evenly. Other algorithms like Floyd–Steinberg dithering avoid clusters and produce much better results.
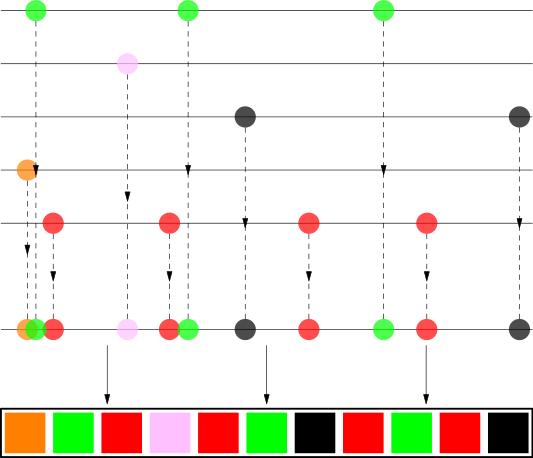
The clusters seen on the previous picture almost fully disappeared. We can take inspiration from the dithering algorithms to solve our problem with clusters of songs by the same artist; we will try to spread them throughout the whole playlist. Suppose we have a playlist containing some songs by The White Stripes, The xx, Bonobo, Britney Spears (Toxic!) and Jaga Jazzist. For each artist we take their songs and try to stretch them as evenly as possible along the whole playlist. Then we collect all songs and order them by their position. A picture is better than a thousand words.
As you can see, songs from an artist are nicely spread out and it looks pretty random to a human eye. Let’s look in more detail how the algorithm works.
- Let’s say we have 4 songs from The White Stripes as in the picture above. This means that they should appear roughly every 25% of the length of the playlist. We spread out the 4 songs along a line, but their distance will vary randomly from about 20% to 30% to make the final order look more random. You should be able to see that the distance between the red circles on the line is not the same.
- We introduce a random offset in the beginning; otherwise all first songs would end up at position 0. You can see that both Britney Spears and Jaga Jazzist only have one song, but the random offset causes them to appear at a random place in the playlist.
- We also shuffle the songs by the same artist among each other. Here we can use Fisher-Yates shuffle or apply the same algorithm recursively, for example we could prevent songs from the same album playing too close to each other.
All in all the algorithm is very simple and it can be implemented in just a couple of lines. It’s also very fast and produces decent results.
Conclusion
The algorithm is now rolled out to everyone using our desktop client and other clients will follow soon. Thanks to everyone who gave feedback on our Community page.
Further reading
- What does randomness look like?, a blog post by Aatish Bhatia
- Clustering illusion on Wikipedia
- A very lucky wind, a radio episode about a couple of interesting random phenomenons
- Dither on Wikipedia
- How Randomness Rules Our World and Why We Cannot See It by Michael Shermer
Tags: randomness, shuffle algorithms, user feedback